Surface Simplification

Algorithm Description

The presented surface simplification algorithm simplifies the input mesh using edge contractions. The edge to be contracted at each step is chosen by trying to minimize the error introduced. If a vertex v represents a set of original vertices V; let F be the set of all original polygonal faces incident upon vertices in V. Then we define error as the sum over all faces in F of the distance between v and the plane of the face. An approximation of this error function is given by the Quadric Error Metric [1]. Each vertex is assigned a quadric error metric based on the planes of the incident faces. At each contraction, instead of recalculating the error over all original faces, we can simply sum the quadric error metric of the two vertices involved. Note this may double (or triple) count some faces, but it works well nonetheless as a fast approximation. Also, in most cases, given a QEM it is possible to solve directly for the point of minimum error.

To implement this efficiently, every edge contraction candidate is put into a queue based on the minimum possible error introduced by contracting that edge. The lowest error edge is contracted at each step, and appropriate modifications are made to contractions still in the queue. However, if an edge contraction is chose that results in a face 'flipping' it's normal around (which generally occurs in regions with lots of nearly planar polygons - contractions may fold triangles over other triangles), then the contraction is not used, but is put back into the queue with a slightly higher error.

Furthermore, the algorithm was made to use color as an additional 3 dimensions over which to consider error by using a 6 dimensional vector (x,y,z,r,g,b) in place of the standard 3 dimensional one (and doing the appropriate things to the math).

Papers:

[1] Michael Garland and Paul Heckbert. Surface Simplification Using Quadric Error Metrics. In SIGGRAPH '97 Proc. Aug 1997.
[2] Michael Garland and Paul Heckbert. Simplifying Surfaces with Color and Texture using Quadric Error Metrics. In IEEE Visualization 98.

Experiments:

I am using surface simplification as a method of identifying major light sources in a scene.

I originally intended to use an extrapolated 3d model of the scene to project color onto, thereby adding information about the size and relative orientation of light sources. Unfortunately, the model I intended to use was highly degenerate (many unconnected incident faces with non-incident vertices); it looks like it will require general vertex pair contraction, additional edge constraints, and some form of smart subdivision to accomplish automatically without destroying the scene.

In the meantime, the results of using 6 dimensional quadric error metrics (x,y,z,r,g,b), can be seen in the figures below. The first sphere uses a projected texture of the interior of St. Peter's Cathedral.

Figures:

St. Peter's Basilica projected onto a sphere and decimated to 8000 faces (click for a larger picture)

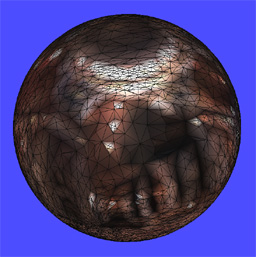
73728 faces	8000 faces

The 'texture' used here is a high-dynamic range texture. Rather than having the colors limited to the range 0-255, the colors are stored as floating point values, representing the actual intensity (and color) of light coming from that direction. The windows in this image have over 1000.0 times the brightness of the rest of the scene; as you can see in the decimated version, the algorithm tries very hard to keep those bright vertices from changing. This effectively isolates the bright light sources, reducing the number of less important (darker) triangles. When calculating the effect of each of these 'light' triangles on an object we are lighting virtually, we are much more interested in the high frequency information of bright spots, and can make do with low frequency information in the dark spots.

A cow, decimated to 1000 and 500 faces:

5804 faces	1000 faces	500 faces

The 1000 face model of the cow, while losing some detail, still retains much of the overall shape. At 500 faces however, the model begins to degrade greatly; we lose the tips of the horns and the shape of the ears.

A spiral color pattern on a curved surface, decimated to 1000 faces:

18050 faces	1000 faces	1000 faces

The vertices on an open 'edge' of a mesh tend to shrink inwards. To fix this, Garland and Heckbert suggest adding additional heavily weighted constraint planes (perpendicular to the edge) to the quadrics of 'edge' vertices. In the interior of the mesh, however, we can see that the decimated version has remained fairly faithful to the color contours.

Face Flipping Edge Contractions Allowed	Face Flipping Edge Contractions Not Allowed

Notice the existence of triangle overlaps in the decimated swirl mesh on the left. When we disallow face flipping edge contractions, (by increasing their error and putting them back in the queue), these overlaps are removed.

A globe color pattern on a sphere, decimated to 8000 faces:

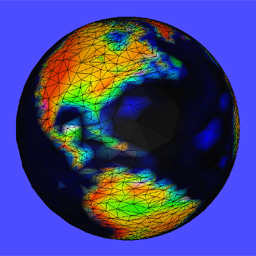
73728 faces	8000 faces	8000 faces

The globe. Note the algorithm tends to prefer smaller triangles near perceived color edges, and decimates the mesh to a greater extent in regions of more constant color.

Timings:

Run on a Pentium II 450 Mhz with 384 MB RAM, running Windows NT 4.0

Win32 Executables:

• SimplifySurface - The Surface Simplifier, [Instructions]
  
• SMFView - Viewer for SMF files, courtesy of Michael Garland [Instructions]
  

Sample Models and Files:

- SMF model of a cow	- SMF model of a cube
- RAD model of St. Peter's Basilica (interior)	- SMF model of a dragon
- SMF model of the globe	- SMF model of a spiral on a curved surface
- Environment Map of St. Peter's Basilica (Low dynamic range jpg)